Deep Learning Programming Style: Symbolic, Imperative

DataScience

📅 January 05, 2018

•

⏱️5 min read

TensorFlow 1.5 버전부터 Eager Execution 이라는 기능이 추가되었습니다. 다시 말해서 imperative programming style을 지원한다고 적혀있는데, 기존의 방식과 어떤 차이가 있는지 알아보겠습니다. MXNet의 Deep Learning Programming Style 문서를 번역한 내용입니다.

Deep Learning Programming Style

우리는 항상 성능과 최적화에 대한 고민을 합니다. 하지만 그 이전에 잘 동작하는 코드인지 여부가 중요합니다. 이제는 다양한 딥러닝 라이브러리들이 존재하지만 각자 프로그래밍 방식에 대해 다른 접근 방식을 가지고 있기 때문에 학습하는 것도 힘들며, 이를 이용하여 명확하고 직관적인 deep learning 코드를 작성하는 것도 어렵습니다.

이 문서에서는 가장 중요한 두 가지 디자인 패턴에 집중하려고 합니다.

Whether to embrace the symbolic or imperative paradigm for mathematical computation.
Whether to build networks with bigger (more abstract) or more atomic operations.

Symbolic vs. Imperative Programs

만일 당신이 파이썬 또는 C++ 개발자라면, 이미 Imperative program과 친숙할 것 입니다. Imperative style program들은 바로 연산을 수행합니다. 대부분의 파이썬 코드들이 imperative 한 형태를 보여주는데, 예를 들면 아래와 같은 Numpy 코드를 말합니다.

import numpy as np
a = np.ones(10)
b = np.ones(10) * 2
c = b * a
d = c + 1

프로그램이 c = b * a를 수행하도록 명령을 내리면, 실제로 연산이 실행됩니다.

반면에 Symbolic program은 조금 다릅니다. Symbolic-style program에서는 먼저 function (potentially complex) 을 정의합니다. function을 정의했다고 해서 실제 연산이 수행되는 것은 아닙니다. 우리는 그저 placeholder 값에 function을 정의한 것 뿐 입니다. 이 과정 이후에 function을 컴파일 할 수 있으며, 실제 입력 값을 통해 이를 평가하게 됩니다. 아래는 위에서 언급했던 imperative 코드를 symbolic style로 변환한 예제입니다.

A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)
# compiles the function
f = compile(D)
d = f(A=np.ones(10), B=np.ones(10)*2)

보시다시피 symbolic 버전에서는 C = B * A가 수행되는 시점에 실제로 연산이 일어나지 않습니다. 대신에 이 operation은 연산 과정을 표현하는 computation graph (aka. symbolic graph) 를 생성합니다. 예를 들면, D의 연산을 위해 아래와 같은 computation graph가 생성됩니다.

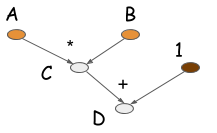
comp graph

대부분의 symbolic-style 프로그램들은 명시적으로든 암시적으로든 컴파일 단계를 포함합니다. 이를 통해 computation graph를 언제든 호출할 수 있는 함수로 변환시켜줍니다. 위의 예제에서도 실제 연산은 코드의 마지막 줄에서만 수행됩니다. 이를 통해 얻을 수 있는 점은 computation graph를 작성하는 단계와 실행하는 단계를 명확히 분리할 수 있다는 것 입니다. Neural Network에서도 우리는 전체 모델을 단일 computation graph로 정의합니다.

Torch, Chiner 그리고 Minerva와 같은 딥러닝 라이브러리들은 imperative style을 사용하고 있습니다. symbolic-style을 사용하는 딥러닝 라이브러리로는 Theano, CGT 그리고 TensorFlow가 있습니다. 그리고 CXXNet 이나 Caffe와 같은 라이브러리들은 설정파일에 의존하는 방식으로 symbolic style을 지원합니다. (ex. Caffe의 prototxt) 이제 두 가지 딥러닝 프로그래밍 방식에 대해 이해했으니, 각 방식의 장점에 대해 알아보겠습니다.

Imperative Programs Tend to be More Flexible

imperative program은 프로그래밍 언어의 flow와 상당히 잘 맞아들어가며 유연하게 동작하는 것 처럼 보입니다. 그렇다면 왜 수 많은 딥러닝 라이브러리들이 symbolic 패러다임을 선택할까요? 가장 큰 이유는 메모리 사용량과 속도 측면에서의 효율성 때문입니다. 위에서 언급했던 예제로 돌아가 천천히 설명드리겠습니다.

a = np.ones(10)
b = np.ones(10) * 2
c = b * a
d = c + 1

comp graph

주어진 array의 각 셀이 8 바이트의 메모리를 소모한다고 가정해보겠습니다. 콘솔에서 위의 프로그램을 실행하면 메모리가 얼마나 소모될까요?

imperative program에서는 각 라인마다 메모리 할당이 요구됩니다. 사이즈가 10인 array가 4개 할당되므로 4 * 10 * 8 = 320 bytes의 메모리가 요구됩니다. 반면 computation graph에서는 궁극적으로 d가 필요하다는 것을 알고 있기 때문에, 즉시 값을 메모리에 할당하는 대신에 메모리를 재사용할 수 있습니다. 예를 들어 b를 위해 할당된 공간에 c를 저장하도록 재사용하고, c를 위해 할당된 공간에 다시 d를 저장하도록 한다면 결국 요구되는 메모리는 2 * 10 * 8 = 160 bytes 절반으로 줄어들게 됩니다.

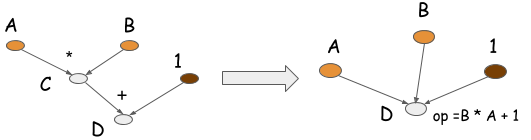
comp graph fold

Symbolic program은 사실 이보다 더 엄격합니다. 우리가 D에 대한 컴파일을 호출하면, 시스템은 오직 d 값이 필요하다는 사실만 인지합니다. 따라서 위와 같은 경우, 즉시 연산에 의해 c는 존재하지 않는 값으로 취급합니다.

symbolic program이 안전하게 메모리를 재사용함으로 인해 우리가 얻는 장점은 분명 있습니다. 하지만, 나중에 우리가 c에 대해 접근해야하는 경우가 생긴다면 난감해집니다. 따라서 imperative program은 모든 가능한 경우의 수에 접근해야 할 때 더 좋은 대안이 될 수 있습니다. 대표적으로 파이썬 콘솔에서 imperative 버전의 코드를 실행시킨다면, 미래에 발생할 수 있는 변수를 중간 과정을 통해 미리 검사할 수 있습니다.

Symbolic program은 operation folding 최적화도 수행해줍니다. 다시 위의 예시를 살펴보면 곱셈과 합 연산이 하나의 operation으로 합쳐지는 것을 그래프를 통해 확인할 수 있습니다. 만일 연산이 GPU 프로세서에 의해 실행된다면, 두 개가 아닌 하나의 GPU 커널만 실행될 것 입니다. 실제로 이는 CXXNet, Caffe와 같은 라이브러리에서 연산을 수행하는 방식입니다. Operation folding 방식은 계산 효율을 향상시켜줍니다.

아시다시피 imperative program에서는 중간 값이 나중에 참조될 수 있기 때문에 operation folding 방식을 수행할 수 없습니다. 반면, computation graph에서는 전체 계산 그래프를 얻을 수 있고 어떤 값을 필요로하는지 알 수 있기 때문에 operation folding이 가능합니다.

Case Study: Backprop and AutoDiff

이제 auto differentiation이나 backpropagation과 같은 문제를 통해 두 가지 프로그래밍 모델을 비교해보겠습니다. (chaining rule이 어떻게 동작하는지 보여주겠다) 미분은 모델을 훈련시키는 메커니즘이기 때문에 딥러닝에 있어 정말 중요합니다. 우선 대부분의 딥러닝 모델에서 loss function을 정의하는데 이는 모델이 예측한 값이 실제 값과 얼마나 멀리 떨어져 있는지를 말합니다. 그리고 나서 훈련 데이터를 모델에게 전달하고, 각 step에서 모델의 parameter를 업데이트하여 loss를 최소화합니다. 즉, parameter가 업데이트 하는 방향은 loss function 결과에 의해 결정됩니다.

comp graph backward

imperative와 symbolic 방식 모두 gradient 계산을 수행할 수 있습니다. 먼저 아래의 파이썬 코드를 통해 imperative program이 어떻게 automatic differentiation을 수행하는지 알아보겠습니다.

class array(object) :
    """
    Simple Array object that support autodiff.
    """
    def __init__(self, value, name=None):
        self.value = value
        if name:
            self.grad = lambda g : {name : g}

    def __add__(self, other):
        assert isinstance(other, int)
        ret = array(self.value + other)
        ret.grad = lambda g : self.grad(g)
        return ret

    def __mul__(self, other):
        assert isinstance(other, array)
        ret = array(self.value * other.value)
        def grad(g):
            x = self.grad(g * other.value)
            x.update(other.grad(g * self.value))
            return x
        ret.grad = grad
        return ret

# some examples
a = array(1, 'a')
b = array(2, 'b')
c = b * a
d = c + 1
print d.value
print d.grad(1)
# Results
# 3
# {'a': 2, 'b': 1}

Model Checkpoints

모델을 저장하고 다시 불러오는 일 또한 중요합니다. 보통 Neural Network 모델을 저장한다는 것은 네트워크의 구조, 설정 값 그리고 weight 값의 저장을 의미합니다.

A = Variable('A')
B = Variable('B')
C = B * A
D = C + Constant(1)

D.save('mygraph')
D2 = load('mygraph')
f = compile([D2])
# more operations
...

설정 값을 체크하는 일은 symbolic program이 더 유리 합니다. symbolic 구조에서는 실제 연산을 수행할 필요가 없기 때문에 computation graph를 그대로 serialize 하면 됩니다. 반면에 Imperative program은 연산 할 때 실행되기 때문에 코드 자체를 설정 파일로 저장하거나 그 위에 또 다른 레이어를 구성해야합니다.

Parameter Updates

computation graph의 경우 연산과정은 쉽게 설명할 수 있지만 parameter 업데이트에 대해서는 명확하지 못합니다. parameter update는 기본적으로 값의 변경(mutation)을 요구하기 때문에 computation graph의 개념과 맞지 않습니다. 따라서 대부분의 symbolic program들은 persistent state를 갱신하기 위해 special update 구문을 사용하고 있습니다.

반면에 imperative style에서는 parameter 업데이트를 작성하는 것이 쉽습니다. 특히 서로 연관된 여러 업데이트가 필요할 때 더욱 그렇습니다. Symbolic program의 경우 업데이트 문은 사용자가 호출 할 때 실행됩니다. 이런 점에서 대부분의 symbolic deep learning 라이브러리는 parameter 업데이트에 대해 gradient 연산을 수행하면서 업데이트를 수행하는 imperative style로 다시 돌아갑니다.

There Is No Strict Boundary

두 가지 프로그래밍 스타일을 비교해서, 하나만 사용하라는 말이 아닙니다. 명령형 프로그램을 상징형 프로그램처럼 만들거나 그 반대도 가능합니다. 예를 들면, Python으로 JIT (just-in-time) 컴파일러를 작성하여 명령형 Python 프로그램을 컴파일 할 수 있습니다. 하지만 두 가지 아키텍쳐를 이해하는 것은 수 많은 딥러닝 라이브러리의 추상화와 그 차이를 이해하는데 도움이 됩니다. 결국, 우리는 프로그래밍 스타일 간에 명확한 경계선이 없다고 결론을 내릴 수 있습니다.

← Prev Next →