포트폴리오의 기대수익률과 변동성 계산

Financial

📅 April 25, 2018

•

⏱️5 min read

흔히 투자자들 사이에 내려오는 격언 중에 **"계란을 한 바구니에 담지 말라"**라는 말이 있습니다. 하나의 자산에 올인하는 것보다 다양한 자산에 분산 투자하여 리스크를 최소화하라는 말입니다.

그렇다면 내가 가진 돈을 어디에 얼마나 배분해야 위험을 낮추고 수익을 최대화 시킬 수 있을까요? 이러한 문제를 자산 배분(Asset Allocation) 문제라고 합니다. 앞으로 자산 배분 전략 중 위험 대비 수익을 장기적으로 최대화하는 방법에 대해 정리해보려 합니다.

단일 자산의 수익률과 변동성 계산

먼저 단일 자산에 대한 수익률과 위험을 정의해야 합니다. 아래의 그래프는 17/09/10 부터 18/03/30 기간의 넷마블, 카카오 종가 그래프입니다.

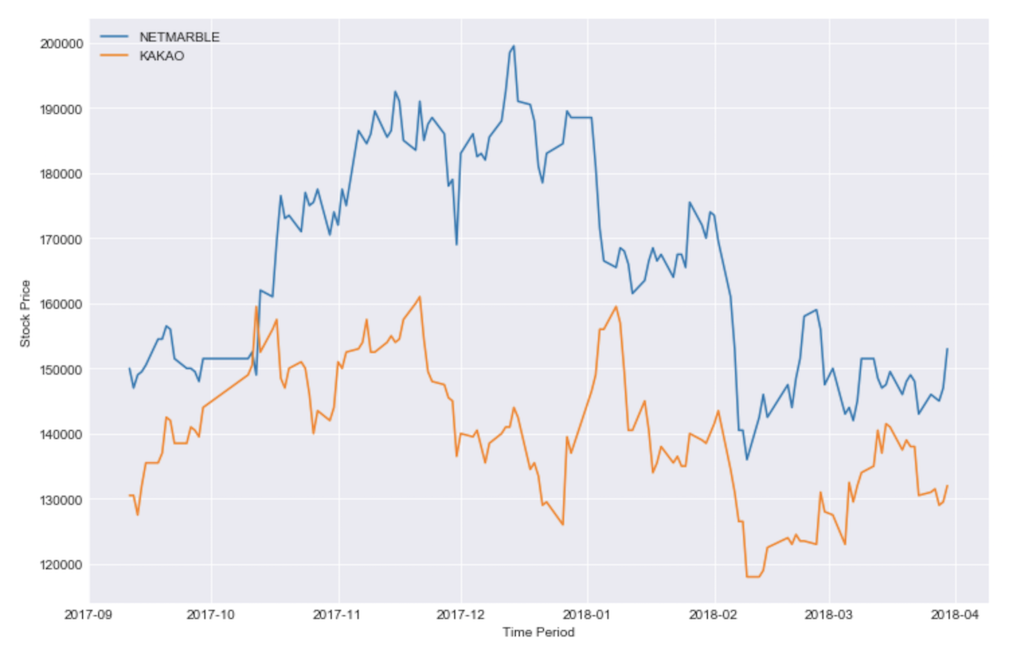
stock ex

넷마블의 기간 수익률은 2%, 카카오는 1%로 비슷하지만 변동성은 눈으로만 봐도 넷마블이 높아보입니다. 포트폴리오 이론에서 위험하다는 것은 변동성이 큰 주식을 의미하며, 같은 수익률을 준다면 변동성이 더 낮은 주식을 선호합니다.

평균 수익률 계산

매수, 매도한 시점을 기준으로 계산하는 기간 수익률은 다들 쉽게 계산합니다. 그렇다면 월 평균 수익률은 어떻게 계산할 수 있을까요? (수수료는 없다고 가정)

아마 대부분 매월 발생하는 수익률의 평균을 떠올릴 것 입니다. 하지만 잘 생각해보면 이 방법은 실제 평균 수익률과 큰 차이가 존재합니다.

예를 들어 1억의 시드를 가지고 1월에 50% 수익, 2월에 30% 손실이 발생했다고 가정해보겠습니다. 최종 금액은 1억 500만원이 되며 위의 방법을 이용한 평균 수익률은 (50 + -30) / 2 = 10%가 됩니다. 하지만 이를 실제로 나누어 계산해보면 실제 수익률과 큰 차이가 존재합니다.

1월에 10% 수익을 얻었다면 1억 1000만원, 2월에는 1억 2100만원이 됩니다. 무려 12100 - 10500 = 1600만원이나 차이가 존재합니다. 이를 제대로 계산하기 위해서는 산술평균이 아닌 기하평균을 사용해야합니다.

$E(R) = \frac{1}{N}\sum_{i=1}^{N}R_i$

$E(R) = \sqrt[N]{R_1 \times R_2... \times R_i}$

첫 번째 수식이 산술평균이고 두 번째 수식이 기하평균입니다. 여기에서 n은 기간이 됩니다. 앞의 예시에 기하평균을 이용해서 평균 수익률을 계산해보면 대략 2.49%가 나옵니다. 이를 이용하여 다시 계산해보면 1월에 1억 249만원, 2월에 1억 504만원이 나옵니다. 오차는 10504 - 10500 = 4만원으로 훨씬 정확하게 나오는 것을 볼 수 있습니다.

변동성 계산

$\sigma^2 = Var(R) = \frac{1}{N-1}\sum_{i=1}^{N}(R_i-\bar{R})$

변동성(=위험)은 기댓값으로 부터 얼마나 떨어져있는지를 나타내는 분산과 동일한 의미를 가집니다. 간단하게 보면 아래의 카카오 종가 그래프에서 평균선과 차이를 모두 더한 값이라고 볼 수 있습니다.

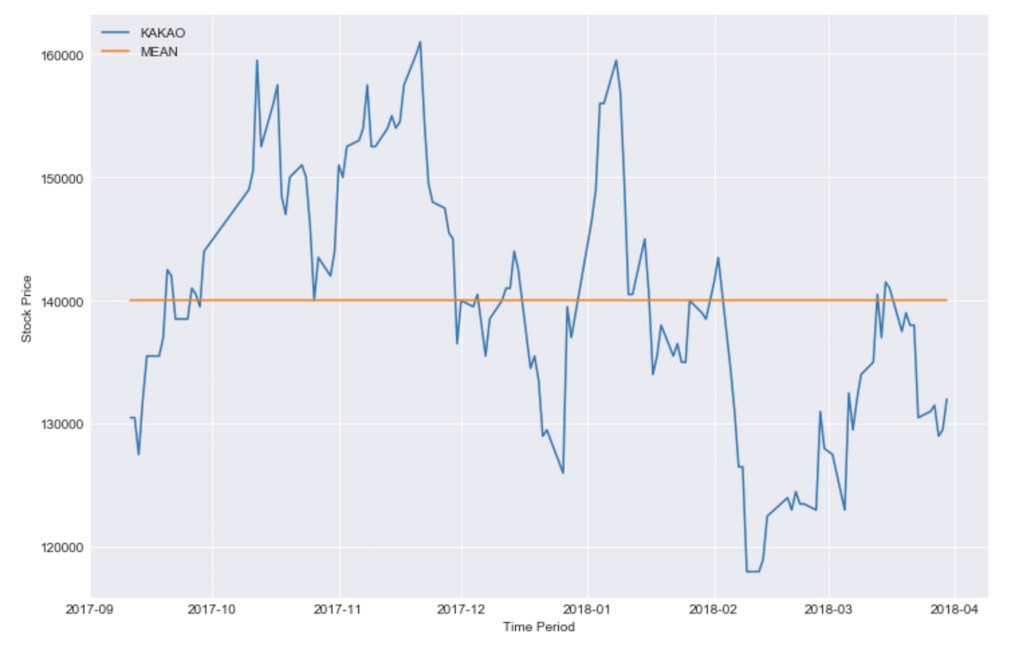
stock var

포트폴리오의 기대수익률과 변동성 계산

처음 설명한 자산 배분 문제는 결국 아래와 같은 과정을 거치게 됩니다.

투자할 자산군을 결정
결정한 자산 별 수익률, 변동성 및 상관관계를 계산
변동성 대비 수익률이 가장 높은 포트폴리오를 구성

$w = portfolio = [w_1, w_2, ... , w_N]^T, where \sum_{i=1}^{N}w_i = 1$

포트폴리오의 경우 앞서 설명한 단일 자산과는 달리 여러 자산으로 구성됩니다. 따라서, 포트폴리오의 기대수익률과 변동성을 계산하려면 주어진 예산에서의 자산 별 투자 비중이 정해져야 합니다.

$\mu_p = portfolio \times expectation = [w_1, w_2, ... , w_N][R_1, R_2, ... , R_N]^T$

포트폴리오의 기대수익률은 개별 자산의 기대수익률과 포트폴리오의 비중을 곱해서 합산하는 방법으로 계산합니다.

$Cov(R^1, R^2) = E[(R^1-\bar{R^1})(R^2-\bar{R^2})] = \frac{1}{N-1}\sum_{i=1}^{N}(R^1-\bar{R^1})(R^2-\bar{R^2})$

포트폴리오의 변동성은 **공분산(Covarience)**을 이용해서 계산할 수 있습니다. 공분산은 확률변수가 2개 이상일 때 각 확률변수들이 얼마나 퍼져있는지를 나타내는 값을 알려주는 지표입니다.

\rho = \cfrac{Cov(X,Y)}{Std(X)Std(Y)}, (-1\leq\rho\leq1)

**상관관계(Correlation Coefficient)**는 확률변수의 절대적 크기에 영향을 받지 않도록 0과 1사이로 단위화시킨 값이라고 보시면 됩니다. 100만원 대의 주식 2개와 10만원 대의 주식 2개의 각 공분산을 계산해보면 100만원 대 주식의 공분산에서 더 큰 값이 나오게 됩니다. 이러한 크기차이에 영향을 받지 않도록 분산의 크기만큼 나눈 것 입니다.

\begin{bmatrix} \sigma_{11} & \sigma_{12} & \cdots & \sigma_{1n} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{n1} & \sigma_{n2} & \cdots & \sigma_{n^2} \end{bmatrix} \begin{bmatrix} w_{1} \\ w_{2} \\ \vdots \\ w_{N} \\ \end{bmatrix}

결국 포트폴리오의 변동성은 포트폴리오의 비중, 투자 자산들 간의 공분산 행렬, 다시 포트폴리오 비중을 곱해 계산할 수 있습니다. 아래는 파이썬의 numpy, pandas, matplotlib을 이용해서 계산하는 노트북 링크입니다. 다음에는 포트폴리오 이론의 시초이자 최적의 mean-varience를 계산하는 markowitz 모델에 대해 정리해보겠습니다.

http://nbviewer.jupyter.org/github/Swalloow/pytrading/blob/master/notebook/portfolio-optimization.ipynb

← Prev Next →